¿Se puede explicar una crisis con matemáticas?

Los hechos ocurridos en nuestro país los últimos 10 días parecen tener variadas causas, razones y explicaciones. Hay consenso que los comportamientos sociales son de extrema complejidad  y de muchísimas variables. Esto nos lleva a la pregunta siguiente: ¿Se puede explicar una crisis con matemáticas?

A primera vista parece imposible, pero las matemáticas pueden ser sorprendentes. A pesar de lo complejo que puede ser un fenómeno, en algunas circunstancias estos pueden ser explicados a partir de ingredientes extremadamente simples. A modo de ejemplo, ya en los años 70, Thomas Schelling y James Sakoda modelaron la segregación social a partir de reglas matemáticas simples aplicadas a fichas blancas y negras sobre un tablero de ajedrez.

En general se pueden identificar dos fases en una crisis social: una fase muy lenta de evolución que eventualmente culmina en una "catástrofe", seguida por una fase de contagio en el comportamiento de la población y su posterior relajación.

La fase de evolución que culmina en "catástrofe" puede ser descrita por una teoría que desarrolló el matemático francés René Thom (Medalla Fields 1958) en 1968, incidentalmente el mismo año que sucedían grandes manifestaciones en la capital francesa: la Teoría de Catástrofes. En pocas palabras, la Teoría de Catástrofes describe la evolución de un proceso, que depende de factores (parámetros) que lo controlan, cuyo comportamiento cualitativo cambia bruscamente (en ese momento sucede la "catástrofe") bajo pequeñas variaciones de los parámetros de control.

La Teoría de Catástrofe se ha aplicado en el ámbito económico, científico y social, por ejemplo para explicar la ocurrencia de "crashes" bursátiles, la transición sólido-líquido-gas de la materia, e incluso para describir cambio en el ánimo de las personas o la esquizofrenia.

En el caso de una crisis social, la Teoría de Catástrofes se puede aplicar para comprender la evolución del estado de tensión social en el que se encuentra una sociedad, la que se puede ver afectada entre otros por factores vinculados a políticas públicas como educación, salud o empleo.

Estos factores pueden incrementar o disminuir esta tensión social y, eventualmente, una variación pequeña puntual en alguno de ellos puede incrementar la tensión social de tal forma, que sucede una "catástrofe", interpretada como un cambio brusco en el comportamiento social de las personas. La palabra catástrofe viene del griego katastrofí y la terminología se usaba para llamar a un evento dramático en una obra de teatro.

[caption id="attachment_890034" align="alignnone" width="318"]

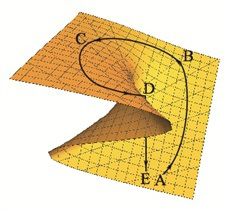
La figura muestra de manera más precisa cómo la catástrofe evoluciona en un gran ciclo de A a D producto de variación de factores como los descritos anteriormente. Este ciclo pasa paulatinamente por las etapas intermedias B y C caracterizadas por

un estado de baja tensión social,

para luego llegar a la etapa D,

que refleja una situación crítica

(por ejemplo de alta tensión social) en la cual la más mínima perturbación es capaz de generar una "catástrofe" pasando el sistema/sociedad bruscamente de D a E. Tal como se aprecia en el gráfico, modificar ligeramente los parámetros en E, como por ejemplo revertir el factor desencadenante de la "catástrofe", no nos lleva de manera fácil y directamente de vuelta a D o a una situación como en C. Así, la rapidez con la que se pueda volver a una situación de menor tensión social, desde A pasando por B y C, va a depender del tipo de medidas implementadas en un determinado contexto social, y eventualmente se podría llegar a una nueva crisis.[/caption]

Luego de la catástrofe puede generarse una fase de contagio del comportamiento social de las personas. Esta ha sido estudiada recientemente por el matemático H. Berestycki, y el físico J.P. Nadal, y sus colaboradores en Francia, quienes lograron describir mediante modelos matemáticos, similares a modelos de transmisión de enfermedades, la propagación de disturbios sucedidos en Francia el 2005.

Estos comenzaron en un barrio periférico vulnerable de París propagándose a toda Francia, por lo que son un ejemplo de un comportamiento colectivo dramático que fue escalando y, en consecuencia, contagiando el comportamiento social a nuevos agitadores a lo largo del país.

Un aspecto interesante de este estudio es que la propagación del disturbio observado en Francia no fue debido al desplazamiento físico de los agitadores, sino que se observa más bien un comportamiento similar al de una onda de propagación de disturbios entre ciudades y localidades, a causa de un evento desencadenante.

Si un evento desencadenante produce o no una onda de propagación y cuál es su extensión geográfica depende de condiciones similares a las necesarias para que se propaga una enfermedad: una densidad lo suficientemente grande de individuos susceptibles (potenciales agitadores), una red de contactos adecuada, y transmisión efectiva de información. Se puede concluir que, si la localidad cero en la que se produce la "catástrofe" tiene localidades vecinas densamente pobladas, entonces se puede esperar un contagio a grande escala del comportamiento observado en la localidad cero, que eventualmente se relaja decayendo.

Es importante estudiar cómo y en qué medida ciertos factores afectan la tensión social y de qué forma sentimientos sociales se transmiten, para de esta forma poder entender la evolución de una crisis y la propagación de disturbios.  El hecho que las comunicaciones mediante redes sociales hoy en día hayan evolucionado significativamente con respecto al 2005, nos hace pensar que se abren nuevas interesantes perspectivas a esta problemática; pero, lo que ya se ha estudiado es que la geografía de un país y su densidad poblacional importan.

* Katia Vogt (matemática) y Sergio Rica (físico), son académicos de la Facultad de Ingeniería y Ciencias U. Adolfo Ibáñez